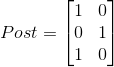Menyelesaikan SPL di matlab
Misal:
x + y + 2z = 9
2x + 4y - 3z = 1
3x + 6y - 5z = 0
Penyelesaian:
Ubah sistem ke dalam bentuk matriks A.c = b
1 1 2 x 9
A = 2 4 -3 c = y b = 1
3 6 -5 z 0
Dalam matlab tuliskan:
A = [1 1 2;2 4 -3;3 6 -5]
b = [9;1;0]
c = inv(A)*b
Maka akan diperoleh hasil sebagai berikut:
yang berarti bahwa nilai x = 1; y = 2; dan z = 3
Rabu, 01 Maret 2017
Ada Apa dengan Perkalian?
Matematika merupakan pelajaran yang telah diberikan sejak memulai pendidikan di bangku sekolah dasar. Materi pelajaran matematika akan semakin meningkat tingkat kesukarannya seiring dengan semakin meningkatnya jenjang pendidikan yang dilalui. Dimulai dari mengenal angka dan operasi hitung bilangan yang sederhana seperti penjumlahan dan pengurangan hingga persoalan matematis yang lebih kompleks.
Menurut pandangan saya, hingga tingkat sekolah dasar harusnya setiap siswa paling tidak sudah mampu untuk melakukan operasi hitung bilangan dengan baik.
Pada tahun 2011 ketika pertama kali saya terjun langsung sebagai guru matematika di salah satu smp swasta di Kota Tarakan, saya dapati bahwa hampir semua siswa tidak mampu berhitung dengan baik, khusunya perkalian. Pada semester selanjutnya masih di tahun yang sama, saya berkesempatan untuk mengajar dijenjang yang lebih tinggi lagi, yaitu jenjang sma. Hal yang sama juga saya temui. Bahkan sekarang pada tahun 2017 ketika saya sudah berhadapan dengan mahasiswa, hal yang sama pun masih saya temui.
Mengapa siswa yang sudah duduk di bangku kuliah, sma, dan smp masih terkendala dalam perkalian?
Bagaimana mungkin mereka bisa lulus di pelajaran matematika pada setiap jenjang pendidikan tanpa hapal perkalian?
Pada waktu saya di sekolah dasar sekitar tahun 1994-2000 perkalian merupakan sesuatu yang betul-betul harus dikuasi. Para guru membimbing dengan berbagai macam cara agar siswanya mampu menghapal perkalian.
Apakah sekarang itu tidak dilakukan?
Maaf, bukan bermaksud offense kepada para guru yang tentunya juga pasti sudah berkerja keras dalam mendidik para siswa. Hanya sekedar pertanyaan dalam hati yang selalu mengganggu pikiran saya yang juga sebagai tenaga pendidik.
Dari informasi yang saya peroleh, ada oknum guru sd yang terkesan hanya memberi catatan dan memberi tugas kepada para siswa. Siswa dipaksa untuk belajar sendiri dan guru terkadang meninggalkan para siswanya.
Mungkin perlu dilakukan penelitian terhadap kecurigaan saya terhadap hal ini. Karena pada akhirnya pada setiap siswa atau pun mahasiswa yang saya temui, mau/tidak mau mereka harus diajarkan lagi/mengulang materi matematika dasar. Akhirnya, capaian pembelajaran mereka selalu tidak sesuai dengan apa yang diharapkan.
Senin, 27 Februari 2017
Lingkaran
Rumus Keliling Lingkaran
k = 2 phi r
k = phi d
Rumus Luas Lingkaran
L = phi r^2
L = 1/4 phi d^2
phi bernilai 22/7 atau 3,14
phi = 22/7 digunakan untuk r atau d yang merupakan bilangan kelipatan 7.
phi = 3,14 digunakan untuk r atau d yang bukan merupakan bilangan kelipatan 7.
bilangan kelipatan 7 adalah bilangan yang dapat dibagi habis oleh 7, yaitu 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140, 147, 154, 161, 168, 175, ... dst.
Contoh 1
Diketahui sebuah jari-jari lingkaran adalah 35 cm. Hilunglah a.) diameter ; b.) keliling ; c.) luas
Jawab:
a.) diameter adalah dua kali jari-jari. Jadi d = 2r = 2(35) = 70 cm.
Karena r = 35 dan 35 merupakan kelipatan 7, maka untuk menghitung keliling dan luas kita gunakan phi = 22/7.
b.) k = 2 phi r = (2)(22/7)(35) = (2)(22)(5) = 220 cm.
atau
k = phi d = (22/7)(70) = (22)(10) = 220 cm.
c.) L = phi r^2 = (22/7)(35)(35) = (22)(5)(35) = 3850 cm^2
atau
L = 1/4 phi d^2 = (1/4)(22/7)(70)(70) = (11)(5)(70) = 3850 cm^2
Contoh 2
Diketahui sebuah jari-jari lingkaran adalah 30 cm. Hilunglah a.) diameter ; b.) keliling ; c.) luas
Jawab:
a.) diameter adalah dua kali jari-jari. Jadi d = 2r = 2(30) = 60 cm.
Karena r = 30 dan 30 bukan merupakan kelipatan 7, maka untuk menghitung keliling dan luas kita gunakan phi = 3,14.
b.) k = 2 phi r = (2)(3,14)(30) = 188,4 cm.
atau
k = phi d = (3,14)(60) = 188,4 cm.
c.) L = phi r^2 = (3,14)(30)(30) = 2826 cm^2
atau
L = 1/4 phi d^2 = (1/4)(3,14)(60)(60) = 2826 cm^2
Lingkaran Dalam Segitiga
Jika a, b, dan c merupakan panjang sisi-sisi suatu segitiga sebarang, maka keliling segitiga tersebut adalah:
k = a + b + c
2s = k = a + b + c
s = (1/2)(k) = (1/2)(a + b + c)
Selanjutnya luas segitiga dapat dihitung dengan menggunakan rumus:
Kemudian r = L/s, sehingga jari-jari lingkaran dalam segitiga dapat dicari dengan menggunakan rumus:
Lingkaran Luar Segitiga
Jari-jari suatu lingkaran luar segitiga dapat dicari dengan menggunakan rumus:
Contoh 3:
Diketahui suatu segitiga sebarang dengan a = 3 cm, b = 4 cm, dan c = 5 cm. Hitunglah jari-jari lingkaran dalam segitiga tersebut!
Jawab:
s = (1/2)(a + b + c) = (1/2)(3 + 4 + 5) = (1/2)(12) = 6 cm.
Jadi, panjang jari-jari lingkaran dalam segitiga tersebut adalah 1 cm.
Contoh 4:
Diketahui suatu segitiga sebarang dengan a = 3 cm, b = 4 cm, dan c = 5 cm. Hitunglah jari-jari lingkaran luar segitiga tersebut!
Jawab:
s = (1/2)(a + b + c) = (1/2)(3 + 4 + 5) = (1/2)(12) = 6 cm.
Jadi, panjang jari-jari lingkaran dalam segitiga tersebut adalah 2 1/2 cm atau 2,5 cm.
Sumber: Buku Matematika Kelas VIII SMP
k = 2 phi r
k = phi d
Rumus Luas Lingkaran
L = phi r^2
L = 1/4 phi d^2
phi bernilai 22/7 atau 3,14
phi = 22/7 digunakan untuk r atau d yang merupakan bilangan kelipatan 7.
phi = 3,14 digunakan untuk r atau d yang bukan merupakan bilangan kelipatan 7.
bilangan kelipatan 7 adalah bilangan yang dapat dibagi habis oleh 7, yaitu 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126, 133, 140, 147, 154, 161, 168, 175, ... dst.
Contoh 1
Diketahui sebuah jari-jari lingkaran adalah 35 cm. Hilunglah a.) diameter ; b.) keliling ; c.) luas
Jawab:
a.) diameter adalah dua kali jari-jari. Jadi d = 2r = 2(35) = 70 cm.
Karena r = 35 dan 35 merupakan kelipatan 7, maka untuk menghitung keliling dan luas kita gunakan phi = 22/7.
b.) k = 2 phi r = (2)(22/7)(35) = (2)(22)(5) = 220 cm.
atau
k = phi d = (22/7)(70) = (22)(10) = 220 cm.
c.) L = phi r^2 = (22/7)(35)(35) = (22)(5)(35) = 3850 cm^2
atau
L = 1/4 phi d^2 = (1/4)(22/7)(70)(70) = (11)(5)(70) = 3850 cm^2
Contoh 2
Diketahui sebuah jari-jari lingkaran adalah 30 cm. Hilunglah a.) diameter ; b.) keliling ; c.) luas
Jawab:
a.) diameter adalah dua kali jari-jari. Jadi d = 2r = 2(30) = 60 cm.
Karena r = 30 dan 30 bukan merupakan kelipatan 7, maka untuk menghitung keliling dan luas kita gunakan phi = 3,14.
b.) k = 2 phi r = (2)(3,14)(30) = 188,4 cm.
atau
k = phi d = (3,14)(60) = 188,4 cm.
c.) L = phi r^2 = (3,14)(30)(30) = 2826 cm^2
atau
L = 1/4 phi d^2 = (1/4)(3,14)(60)(60) = 2826 cm^2
Lingkaran Dalam Segitiga
Jika a, b, dan c merupakan panjang sisi-sisi suatu segitiga sebarang, maka keliling segitiga tersebut adalah:
k = a + b + c
2s = k = a + b + c
s = (1/2)(k) = (1/2)(a + b + c)
Selanjutnya luas segitiga dapat dihitung dengan menggunakan rumus:
Kemudian r = L/s, sehingga jari-jari lingkaran dalam segitiga dapat dicari dengan menggunakan rumus:
Lingkaran Luar Segitiga
Jari-jari suatu lingkaran luar segitiga dapat dicari dengan menggunakan rumus:
Contoh 3:
Diketahui suatu segitiga sebarang dengan a = 3 cm, b = 4 cm, dan c = 5 cm. Hitunglah jari-jari lingkaran dalam segitiga tersebut!
Jawab:
s = (1/2)(a + b + c) = (1/2)(3 + 4 + 5) = (1/2)(12) = 6 cm.
Jadi, panjang jari-jari lingkaran dalam segitiga tersebut adalah 1 cm.
Contoh 4:
Diketahui suatu segitiga sebarang dengan a = 3 cm, b = 4 cm, dan c = 5 cm. Hitunglah jari-jari lingkaran luar segitiga tersebut!
Jawab:
s = (1/2)(a + b + c) = (1/2)(3 + 4 + 5) = (1/2)(12) = 6 cm.
Jadi, panjang jari-jari lingkaran dalam segitiga tersebut adalah 2 1/2 cm atau 2,5 cm.
Sumber: Buku Matematika Kelas VIII SMP
Petri Net dan Hybrid Petri Net
PETRI NET
Petri Net adalah 4-tuple (P, T, A, w) dengan
Petri Net (PN) pada gambar di atas terdiri dari dua place, yaitu p1 dan p2. Atau dapat kita tulis P = {p1, p2}. Pada gambar tersebut juga terdapat dua transisi, yaitu t1 dan t2. Atau dapat kita tulis T = {t1, t2}. Arc dinyatakan dalam pasangan berurutan. Elemen pertama menyatakan asal dan elemen kedua menyatakan tujuan. Misal, arc dari place p1 ke transisi t1 ditulis (p1, t1), arc dari transisi t1 ke place p2 ditulis (t1, p2), arc dari place p2 ke transisi t2 ditulis (p2, t2), dan arc dari transisi t2 ke place p1 ditulis (t2, p1). Secara lengkap ditulis A = {(p1, t1), (t1, p2), (p2, t2), (t2, p1)}. Bobot arc dari place p1 ke transisi t1 adalah satu, yaitu w(p1, t1) = 1. Karena semua arc berbobot satu pada gambar tersebut, dapat kita tulis w(p1, t1) = w(t1, p2) = w(p2, t2) = w(t2, p1) = 1.
HYBRID PETRI NET
Hybrid Petri Net bertanda adalah 6-tuple R= {P, T, Pre, Post, m0, h} dimana,
Dari gambar tersebut dapat kita ketahui bahwa P = {p3, p4, p5} dan T = {t3, t4} dengan place p4 dan place p5, serta transisi t3dan transisi t4 adalah bagian kontinu dan place p3 adalah bagian diskrit. Bagian diskrit pada gambar ditandai dengan single line sedangkan bagian konitnu pada gambar ditandai dengan double line. Selanjutnya, Pre dan Post diperoleh sebagai berikut:
Baris pada matriks menyatakan place dan kolom pada matriks menyatakan transisi. Angka satu menyatakan bobot arc antara place dan transisi yang terhubung, sedangkan angka nol menyatakan bahwa place dan transisi tidak terhubung.
Matriks Pre menyatakan arc dari suatu place ke suatu transisi. Baris 1 dari matriks Pre menyatakan bahwa terdapat arc dari place p3 ke transisi t3 dengan bobot satu dan tidak terdapat arc dari place p3 ke transisi t4. Baris 2 dari matriks Pre menyatakan bahwa terdapat arc dari place p4 ke transisi t3 dengan bobot satu dan tidak terdapat arc dari place p4 ke transisi t4. Baris 3 dari matriks Pre menyatakan bahwa terdapat arc dari place p5 ke transisi t4 dengan bobot satu dan tidak terdapat arc dari place p5 ke transisi t3.
Matriks Post menyatakan arc dari suatu transisi ke suatu place. Kolom 1 dari matriks Post menyatakan bahwa terdapat arc dari transisi t3 ke place p3 dan place p5 dengan bobot satu dan tidak terdapat arc dari transisi t3 ke place p4. Kolom 2 dari matriks Post menyatakan bahwa terdapat arc dari transisi t4 ke place p4 dengan bobot satu dan tidak terdapat arc dari transisi t4 ke place p3 dan place p5.
Karena P = {p3, p4, p5}, maka m0 = {1, 64, 0} yang berarti bahwa terdapat satu token di place p3, terdapat marking sebesar 64 di place p4 dan tidak terdapat marking di place p5. token dan marking adalah istilah penandaan di PN dan HPN.
Sumber:
Petri Net adalah 4-tuple (P, T, A, w) dengan
- P: himpunan berhingga place, P = {p1, p2, p3, ..., pn}
- T: himpunan berhingga transisi, T = {t1, t2, t3,..., tn}
- A: himpunan arc
- w: fungsi bobot
Petri Net (PN) pada gambar di atas terdiri dari dua place, yaitu p1 dan p2. Atau dapat kita tulis P = {p1, p2}. Pada gambar tersebut juga terdapat dua transisi, yaitu t1 dan t2. Atau dapat kita tulis T = {t1, t2}. Arc dinyatakan dalam pasangan berurutan. Elemen pertama menyatakan asal dan elemen kedua menyatakan tujuan. Misal, arc dari place p1 ke transisi t1 ditulis (p1, t1), arc dari transisi t1 ke place p2 ditulis (t1, p2), arc dari place p2 ke transisi t2 ditulis (p2, t2), dan arc dari transisi t2 ke place p1 ditulis (t2, p1). Secara lengkap ditulis A = {(p1, t1), (t1, p2), (p2, t2), (t2, p1)}. Bobot arc dari place p1 ke transisi t1 adalah satu, yaitu w(p1, t1) = 1. Karena semua arc berbobot satu pada gambar tersebut, dapat kita tulis w(p1, t1) = w(t1, p2) = w(p2, t2) = w(t2, p1) = 1.
HYBRID PETRI NET
Hybrid Petri Net bertanda adalah 6-tuple R= {P, T, Pre, Post, m0, h} dimana,
- P adalah himpunan place yang berhingga dan merupakan himpunan tak kosong,
- T adalah himpunan transisi yang berhingga dan merupakan himpunan tak kosong,
- Pre adalah fungsi input incidence,
- Post adalah fungsi output incidence,
- m0 adalah marking awal,
- h disebut fungsi hybrid yang menggambarkan sebuah node adalah kontinu atau diskrit.
Dari gambar tersebut dapat kita ketahui bahwa P = {p3, p4, p5} dan T = {t3, t4} dengan place p4 dan place p5, serta transisi t3dan transisi t4 adalah bagian kontinu dan place p3 adalah bagian diskrit. Bagian diskrit pada gambar ditandai dengan single line sedangkan bagian konitnu pada gambar ditandai dengan double line. Selanjutnya, Pre dan Post diperoleh sebagai berikut:
Baris pada matriks menyatakan place dan kolom pada matriks menyatakan transisi. Angka satu menyatakan bobot arc antara place dan transisi yang terhubung, sedangkan angka nol menyatakan bahwa place dan transisi tidak terhubung.
Matriks Pre menyatakan arc dari suatu place ke suatu transisi. Baris 1 dari matriks Pre menyatakan bahwa terdapat arc dari place p3 ke transisi t3 dengan bobot satu dan tidak terdapat arc dari place p3 ke transisi t4. Baris 2 dari matriks Pre menyatakan bahwa terdapat arc dari place p4 ke transisi t3 dengan bobot satu dan tidak terdapat arc dari place p4 ke transisi t4. Baris 3 dari matriks Pre menyatakan bahwa terdapat arc dari place p5 ke transisi t4 dengan bobot satu dan tidak terdapat arc dari place p5 ke transisi t3.
Matriks Post menyatakan arc dari suatu transisi ke suatu place. Kolom 1 dari matriks Post menyatakan bahwa terdapat arc dari transisi t3 ke place p3 dan place p5 dengan bobot satu dan tidak terdapat arc dari transisi t3 ke place p4. Kolom 2 dari matriks Post menyatakan bahwa terdapat arc dari transisi t4 ke place p4 dengan bobot satu dan tidak terdapat arc dari transisi t4 ke place p3 dan place p5.
Karena P = {p3, p4, p5}, maka m0 = {1, 64, 0} yang berarti bahwa terdapat satu token di place p3, terdapat marking sebesar 64 di place p4 dan tidak terdapat marking di place p5. token dan marking adalah istilah penandaan di PN dan HPN.
Sumber:
- David, R., Alla, H., (2010), Discrete, Continuous, and Hybrid Petri Nets, 2nd edition, Springer, Berlin.
- Murdianto, D., (2016), Tesis: Pemodelan Instalasi Pengolahan Air Dengan Menggunakan Hybrid Petri Net, Institut Teknologi Sepuluh Nopember, Surabaya.
- Subiono, (2015), Aljabar Min-Max Plus dan Terapannya, Institut Teknologi Sepuluh Nopember, Surabaya.
Instalasi Pengolahan Air (IPA) PDAM Kota Tarakan
Pengolahan air yang dilakukan oleh PDAM terdiri dari beberapa proses, seperti pengolahan air pada umumnya. Setiap proses pengolahan dilakukan pada bak penampungan yang berbeda. Secara umum terdapat enam bak dalam sistem pengolahan air bersih, yaitu bak air baku, bak koagulasi, bak flokulasi, bak sedimentasi, bak filtrasi, dan bak air bersih/ reservoir. Masing-masing bak pengolahan memiliki kapasitas dan lamanya waktu pengolahan yang berbeda. Pompa-pompa yang digunakan dalam instalasi pengolahan air juga memiliki keterbatasan waktu dalam pengoperasiannya. Setiap komponen yang saling berkaitan tersebut harus didesain sedemikian rupa sehingga dapat mengolah air baku dan menghasilkan air bersih sesuai dengan kebutuhan konsumen.
Pada gambar di atas terdapat pompa yang terletak di bak intake dan bak reservoir. Pompa ini hanya dapat digunakan jika terdapat air pada masing-masing bak tersebut, sebaliknya jika tidak terdapat air maka pompa tidak dioperasikan. Kemudian terdapat tujuh bak yang digunakan untuk mengambil air baku, mengolah air baku dan menyimpan air bersih, yaitu bak intake, bak koagulasi, bak flokulasi, bak sedimentasi, bak filtrasi, bak desinfektan, dan bak ground reservoir. Masing-masing bak tersebut mempunyai ukuran dan fungsi yang berbeda.
Bak intake merupakan bak pertama yang harus dilalui air baku yang akan diolah menjadi air bersih, ukuran bak ini sekitar 64 meter kubik. Setelah terdapat air di bak intake, maka pompa dapat dioperasikan. Kemudian air dari bak intake ini dipompa ke bak koagulasi. Di bak koagulasi air baku dicampur dengan bahan kimia yang telah ditentukan konsentrasinya terlebih dahulu sebelum proses pengolahan air berlangsung. Penambahan bahan kimia ini menggunakan pipa kecil yang terletak di bagian atas bak koagulasi. Volume bak koagulasi ini adalah 24 meter kubik. Dengan menggunakan beda tinggi air selanjutnya menuju ke bak flokulasi. Di dalam bak ini terdapat sekat-sekat berjarak sekitar 10 cm sehingga air akan mengalir secara zig-zag dan perlahan sehingga membentuk flok. Volume air yang mampu tertampung dalam bak flokulasi ini sekitar 44.5 meter kubik.
Selanjutnya air akan masuk ke bak sedimentasi, di IPA ini bak sedimentasi dibagi menjadi tiga bak dengan ukuran yang sama, yaitu sebesar 33 meter kubik. Namun di dalam bak sedimentasi ini terdapat tube settler yang digunakan untuk memisahkan kotoran flok yang telah terbentuk di bak sebelumnya dengan air bersih, sehingga volume air yang dapat tertampung di bak ini hanya sekitar 25 meter kubik.
Kemudian air akan mengalir ke bak filtrasi dengan menggunakan beda tinggi dari bak sebelumnya. Terdapat empat bak filtrasi dengan ukuran yang sama yaitu sebesar 37.5 meter kubik. Di bak ini terjadi proses penyaringan air dengan menggunkan batu koral, pasir silika, dan karbon aktif. Selanjutnya air dari bak filtrasi akan mengalir ke bak desinfektan yang mempunyai volume relatif lebih kecil dibandingkan dengan bak-bak pengolahan lainnya yaitu sebesar 18 meter kubik. Di bak desinfektan air hasil pengolahan ditambahkan lagi dengan bahan kimia untuk menjamin kualitas air hasil pengolahan. Air bersih hasil pengolahan selanjutnya disimpan di bak ground reservoir. Bak ground reservoir ini terbagi menjadi dua bagian dengan volume total 675 meter kubik.
Pada bak ground reservoir terdapat pompa distribusi yang digunakan untuk mendistribusikan air bersih ke konsumen. Ada dua cara yang digunakan PDAM Kota Tarakan untuk mendistribusikan air bersih, yaitu dengan metode langsung dan metode tidak langsung. Metode langsung dilakukan dengan cara mengalirkan langsung air bersih dari ground reservoir ke pipa konsumen. Motode tidak langsung dilakukan dengan cara memompa terlebih dahulu air bersih dari bak ground reservoir ke bak elevated reservoir yang terletak di Gunung Karang Anyar agar memiliki gaya tekan yang lebih besar untuk selanjutnya dialirkan ke rumah konsumen.
Sumber:
Pada gambar di atas terdapat pompa yang terletak di bak intake dan bak reservoir. Pompa ini hanya dapat digunakan jika terdapat air pada masing-masing bak tersebut, sebaliknya jika tidak terdapat air maka pompa tidak dioperasikan. Kemudian terdapat tujuh bak yang digunakan untuk mengambil air baku, mengolah air baku dan menyimpan air bersih, yaitu bak intake, bak koagulasi, bak flokulasi, bak sedimentasi, bak filtrasi, bak desinfektan, dan bak ground reservoir. Masing-masing bak tersebut mempunyai ukuran dan fungsi yang berbeda.
Bak intake merupakan bak pertama yang harus dilalui air baku yang akan diolah menjadi air bersih, ukuran bak ini sekitar 64 meter kubik. Setelah terdapat air di bak intake, maka pompa dapat dioperasikan. Kemudian air dari bak intake ini dipompa ke bak koagulasi. Di bak koagulasi air baku dicampur dengan bahan kimia yang telah ditentukan konsentrasinya terlebih dahulu sebelum proses pengolahan air berlangsung. Penambahan bahan kimia ini menggunakan pipa kecil yang terletak di bagian atas bak koagulasi. Volume bak koagulasi ini adalah 24 meter kubik. Dengan menggunakan beda tinggi air selanjutnya menuju ke bak flokulasi. Di dalam bak ini terdapat sekat-sekat berjarak sekitar 10 cm sehingga air akan mengalir secara zig-zag dan perlahan sehingga membentuk flok. Volume air yang mampu tertampung dalam bak flokulasi ini sekitar 44.5 meter kubik.
Selanjutnya air akan masuk ke bak sedimentasi, di IPA ini bak sedimentasi dibagi menjadi tiga bak dengan ukuran yang sama, yaitu sebesar 33 meter kubik. Namun di dalam bak sedimentasi ini terdapat tube settler yang digunakan untuk memisahkan kotoran flok yang telah terbentuk di bak sebelumnya dengan air bersih, sehingga volume air yang dapat tertampung di bak ini hanya sekitar 25 meter kubik.
Kemudian air akan mengalir ke bak filtrasi dengan menggunakan beda tinggi dari bak sebelumnya. Terdapat empat bak filtrasi dengan ukuran yang sama yaitu sebesar 37.5 meter kubik. Di bak ini terjadi proses penyaringan air dengan menggunkan batu koral, pasir silika, dan karbon aktif. Selanjutnya air dari bak filtrasi akan mengalir ke bak desinfektan yang mempunyai volume relatif lebih kecil dibandingkan dengan bak-bak pengolahan lainnya yaitu sebesar 18 meter kubik. Di bak desinfektan air hasil pengolahan ditambahkan lagi dengan bahan kimia untuk menjamin kualitas air hasil pengolahan. Air bersih hasil pengolahan selanjutnya disimpan di bak ground reservoir. Bak ground reservoir ini terbagi menjadi dua bagian dengan volume total 675 meter kubik.
Pada bak ground reservoir terdapat pompa distribusi yang digunakan untuk mendistribusikan air bersih ke konsumen. Ada dua cara yang digunakan PDAM Kota Tarakan untuk mendistribusikan air bersih, yaitu dengan metode langsung dan metode tidak langsung. Metode langsung dilakukan dengan cara mengalirkan langsung air bersih dari ground reservoir ke pipa konsumen. Motode tidak langsung dilakukan dengan cara memompa terlebih dahulu air bersih dari bak ground reservoir ke bak elevated reservoir yang terletak di Gunung Karang Anyar agar memiliki gaya tekan yang lebih besar untuk selanjutnya dialirkan ke rumah konsumen.
Sumber:
- Murdianto, D. (2016). Tesis: Pemodelan Instalasi Pengolahan Air Bersih Menggunakan Hybrid Petri Net, ITS, Surabaya.
- PDAM Kota Tarakan.
Minggu, 26 Februari 2017
Analisis Korelasi Pearson
Salah satu teknik satatistik yang kerap kali digunakan untuk mencari hubungan antara dua variabel atau lebih adalah teknik korelasi. Dua variabel yang hendak diselidiki hubungannya tersebut biasanya diberi simbol variabel X dan variabel Y.
Bila mana kenaikan nilai variabel X selalu disertai kenaikan variabel Y, dan turunnya nilai variabel X juga selalu diikuti oleh turunnya nilai variabel Y, maka hubungan yang seperti itu disebut hubungan yang positif. Akan tetapi, sebaliknya bilamana kenaikan nilai variabel X selalu diikuti oleh penurunan nilai variabel Y, dan penurunan nilai variabel X justru diikuti oleh kenaikan nilai variabel Y, maka hubungan antara variabel X dan Y tersebut adalah hubungan yang negatif.
Di samping itu, dua variabel X dan Y ada kemungkinannya tidak memiliki hubungan sama sekali, yakni bilamana kenaikan nilai variabel yang satu kadang-kadang diikuti penurunan nilai variabel lainnya, dan kadang-kadang juga diikuti oleh kenaikan nilai variabel yang lainya.
KOEFISIEN HUBUNGAN
Pada umumnya besar kecilnya hubungan dinyatakan dengan bilangan. Bilangan yang menytatakan besar kecilnya hubungan tersebut disebut koefisien hubungan atau koefisien korelasi. Nilai koefisien korelasi bervariasi, dari -1 sampai dengan +1. Jika nilai koefisien korelasi r positif, maka X dan Y meningkat atau menurun secara bersama. Nilai r = +1 mengindikasikan bahwa hubungan variabel X dan Y adalah sempurna (perfect positive correlation). Ketika r negatif, maka X dan Y bergerak pada arah yang berlawanan. Jika koefisien korelasi r = -1, maka hubungan variabel X dan Y adalah sempurna (perfect negative correlation), dan ketika koefisien korelasi r = 0, maka kedua variabel tidak berkorelasi.
KORELASI PRODUCT MOMENT
Untuk menerapkan koefisien korelasi antara dua variabel yang masing-masing mempunyai skala pengukuran interval maka digunakan korelasi product moment yang dikembangkan oleh Karl Pearson. Rumus korelasi product momen ini ada dua macam, yaitu:
1. Korelasi product moment dengan rumus simpangan (deviasi).
Contoh 1: Mencari koefisien korelasi antara nilai matematika dengan nilai fisika yang diperoleh siswa.

2. Korelasi Product moment dengan
rumus angka kasar.
Dengan contoh yang sama seperti Contoh 1:

INTERPRETASI HARGA r
Interpretasi terhadap harga atau koefisien korelasi secara konvensional diberikan oleh Guilford (1956) sebagai berikut:
Di samping itu, untuk
menafsirkan harga r
(koefisien korelasi)
maka
dapat dikonsultasikan (dibandingkan) dengan harga kritik
r product moment (tabel r).
Dalam hal ini, ditentukan tingkat kesalahan (peluang galat) adalah 5% (yang biasa digunakan pada ilmu-ilmu sosial) dengan melihat pada tabel r berdasarkan N = banyaknya responden. Contoh: pada perhitungan korelasi product moment dimuka diperoleh harga r = 0,745.
Harga r kritik (r tabel) pada tingkat kesalahan 5% dan N = 10 adalah r tab = 0,632. Berarti harga r yang diperoleh dari perhitungan (r hit) = 0,745 > r tab = 0,632. Hal ini menunjukkan bahwa korelasi antara dua variabel tersebut "berarti" (signifikan). Jika r hitung ternyata < r tabel maka dikatakan bahwa korelasi antara kedua variabel tersebut "tidak berarti" (tidak signifikan). Jadi, meskipun ada korelasi tetapi secara statistik kurang berarti
UJI SIGNIFIKANSI r
Untuk menuji signifikansi koefisien korelasi (nilai r) yang diperoleh maka dapat dilakukan sebagai berikut:
- Dengan mengacu pada kriteria koefisien korelasi yang diberikan oleh Guilford (1956).
- Dengan membandingkan nilai r hitung dengan harga r tabel dengan taraf kesalahan (α = 0,05) atau α = 0,01 dan db = N - 2.
- Dengan menghitung lebih dulu t hitung berdasarkan harga r hitung yang diperoleh, yakni dengan rumus sebagai berikut (untuk korelasi product moment):
Harga t hitung yang diperoleh selanjutnya dikonsultasikan dengan harga t tabel dengan taraf signifikansi tertentu (misal : α = 0,05 atau α = 0,01) dan dengan derajat kebebasan dk = N - 2.
Bila t hit > t tabel → maka tolak Ho, dan berarti menerima Ha. Sedangkan bila t hit < t tabel,
maka tidak menolak
Ho,
yang berarti
menolak Ha.
Sumber:
- https://winalmuslim.files.wordpress.com/2014/02/korelasi-pearson.pdf
- Karo-Karo Sitepu, Rasidin dan M. Sinaga, Bonar (2006): Aplikasi Model Ekonometrika: Estimasi, Simulasi dan Peramalan Menggunakan Program SAS. Prorgam Studi Ilmu Ekonomi Pertanian Sekolah Pascasarjana IPB, Bogor.
Langganan:
Komentar (Atom)